- This work has been presented as a highlighted poster in the AGU 2023. Download Poster PDF
Abstract
With the development of the frequency-Bessel transform (F-J) method, multimodal surface wave imaging has become a state-of-the-art approach in ambient noise tomography. Surface wave dispersion curves are derived by integrating empirical Green’s functions (EGFs) across interarray spacing in seismic arrays. To improve the dispersion curve results, EGFs are obtained by stacking ambient noise correlations. The conventional linear stacking (LS) method stacks all short-duration cross-correlation functions (CCFs) over an extended time span to create the final stacks. Moreover, nonlinear stacking methods have been devised for effectiveness. However, the suitability of applying these nonlinear stacking methods to the F-J method remains uncertain, as the F-J method utilizes complete EGF waveforms, which might be altered by certain nonlinear stacking procedures. In this study, we investigate the impact of three common nonlinear stacking methods—phase-weight stacking (PWS) (Schimmel & Paulssen, 1997), root-mean-square ratio selection stacking (RMSS_SS) (Xie et al., 2020), and frequency domain probability selection stacking (FPS) (Liu et al., 2016)—on dispersion spectrogram quality compared with linear stacking (LS) results. The comparative analysis results reveal that while PWS significantly enhances the EGF waveform quality, it contaminates dispersion spectrograms. RMSS_SS moderately affects both EGF waveforms and dispersion spectrograms. However, FPS marginally improves the EGF signal-to-noise ratio (SNR) while greatly enhancing the dispersion spectrogram. Hence, we conclude that the FPS method is the most suitable nonlinear stacking approach for the F-J method.
The F-J Method
The F-J method utilizes a Bessel function integration to reveal the dispersion spectrogram (\(I(\omega,k)\)) from the CCFs in the frequency domain (\(C(\omega,k)\)):
\[I(\omega,k) = \int_0^{+\infty}C(\omega,k)\cdot J_0(kr)rdr\]Where \(\omega\) is the angular frequency, r is the epicentral distance, k is the wavenumber, and \(J_0(kr)\) is the first kind of zeroth-order Bessel function. The dispersion curves can be estimated from the local maximum of the dispersion spectrogram. In addition to the fundamental mode, it can effectively retrieve overtone dispersion curves (Wang et al., 2019) and even leaking modes (Li et al., 2021).
Results on USArray:
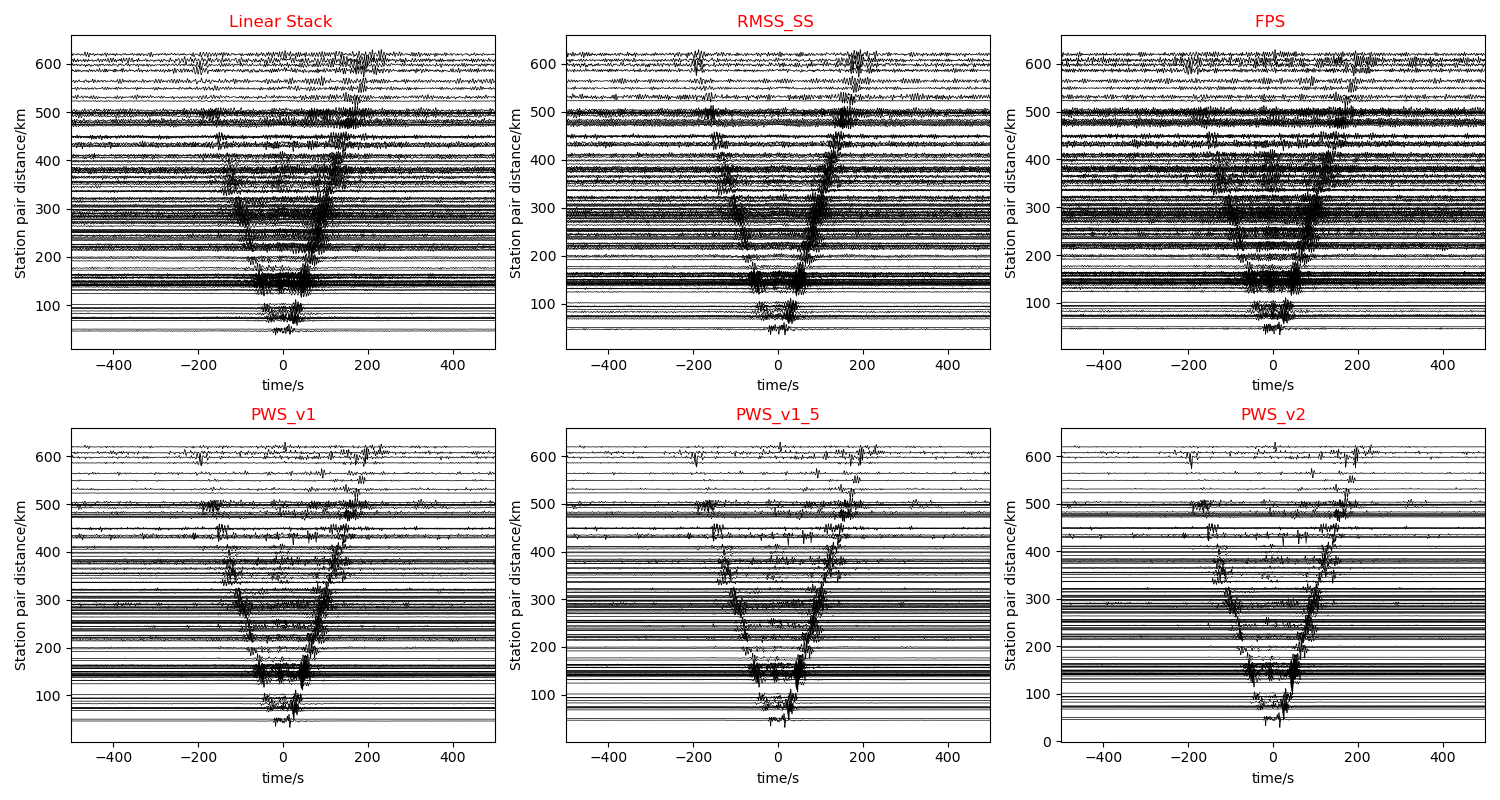
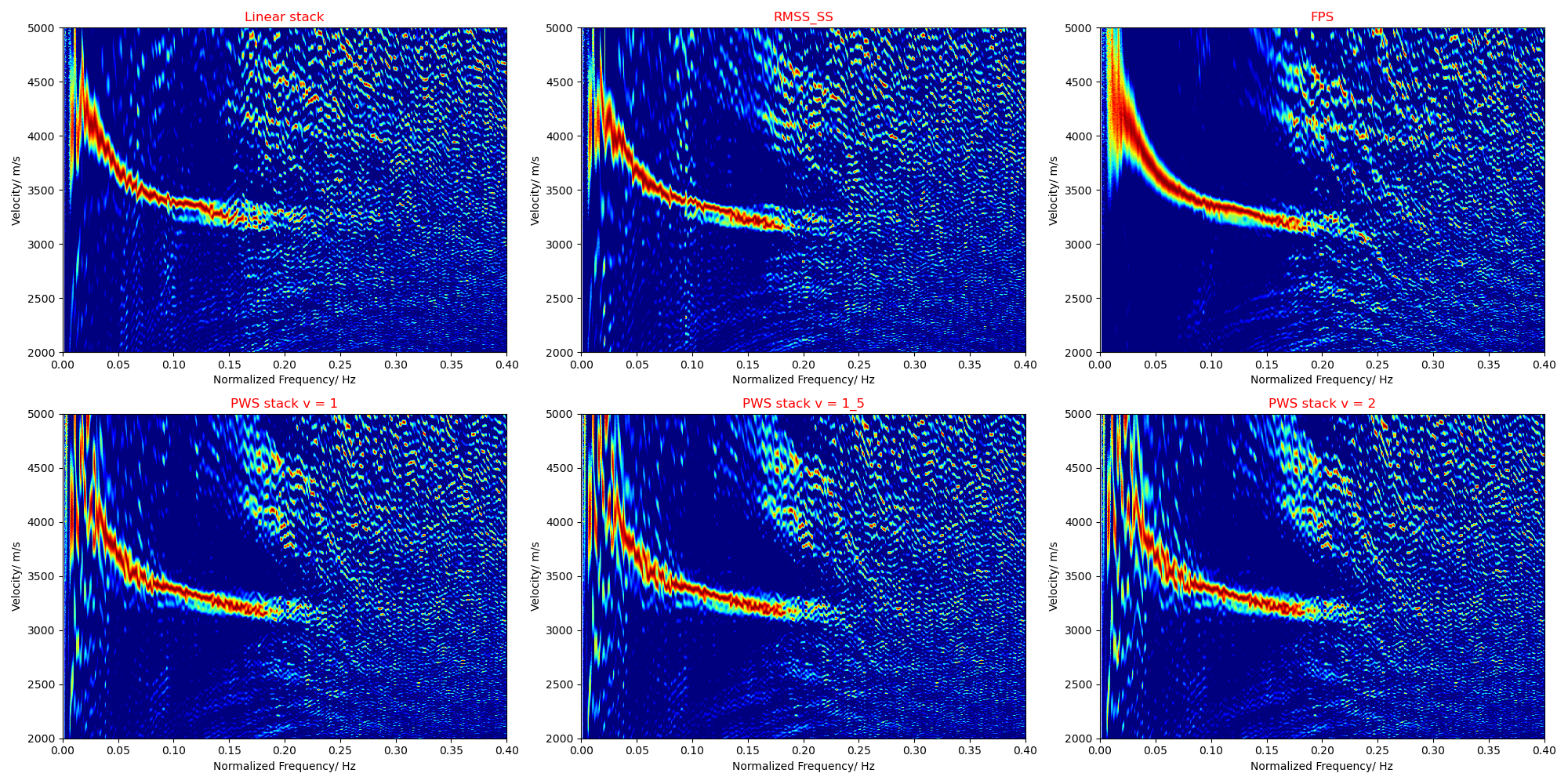

Breif Summary
- PWS significantly improves the SNR of CCFs, while dramatically damages the dispersion spectrogram quality. (Note that the curves in the dispersion spectrograms of PWS are not overtones but artifacts)
- RMSS has a mild influence on both CCFs and dispersion spectrogram, which can remove some strait artifacts.
- FPS has a slight improvement on CCFs’ SNR, while enhancing the resolution and continuity of multimodal.