- Notice: This work is still ongoing. Currently, I have some ideas and am in the process of designing experiments to verify them. Updates will be posted here once I obtain interesting results. The methodology will be shared once it has proven useful and is in a peer-review state due to competitive concerns.
Motivation
Surface wave dispersion curves can be derived by integrating empirical Green’s functions (EGFs) across interarray spacing in seismic arrays. In the context of ambient noise, EGFs are obtained from ambient noise cross-correlation functions (CCFs) (Bensen et al., 2007). To improve the quality of EGFs, numerous strategies have been developed to process the raw CCFs, including linear and nonlinear stacking of CCF segments, preprocessing with prewhitening or one-bit methods, and noise-source-related analyses. Here, we refer to all these CCF-related processes as CCF correction.
Currently, there are still controversial arguments regarding different correction methods, and some of which require extensive calculations and predominantly focus on extracting surface waves of the fundamental mode. With the development of the frequency-Bessel transform (F-J) method (Wang et al., 2019), multimodal surface wave imaging has emerged as a state-of-the-art approach in ambient noise tomography. As indicated by our previous stacking analysis , while useful, it has not significantly improved the dispersion spectrogram for overtones. Therefore, this project aims to develop new correction strategies for CCFs to streamline the need for high-quality EGFs in multimodal surface wave tomography.
Traditional CCFC (TCCFC)
The currently standard processing procedures of the F-J method, referred to as traditional cross-correlation function correlation TCCFC, include the following steps:
- Remove the mean, trend, and instrument response from the raw data.
- Apply pre-whitening and one-bit normalization in both the time and frequency domains.
- Calculate cross-correlation after segmenting the signals.
- Directly stack all CCF segments, known as Linear Stacking (LS).
Updates 1.0 for CCFC_1:
- I developed and tested two new CCF correction strategies with a similar conceptual approach, which we will refer to as CCFC_1-1 and CCFC_1-2. This post shares the inspiring results of our test of CCFC_1-1 and CCFC_1-2 in a dense array. (Update at 2024/10/10)
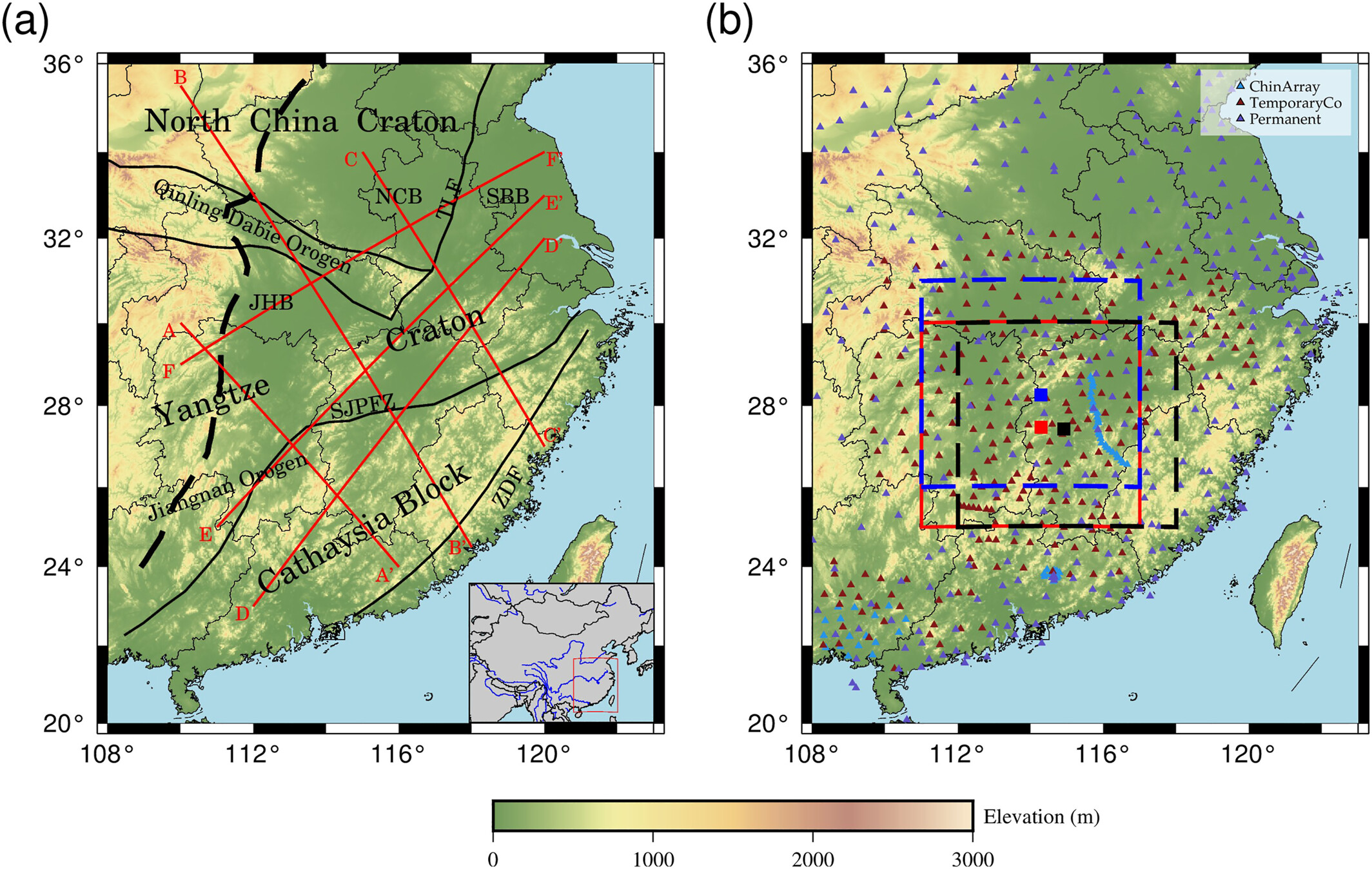
- This test was on seismic arryas deployed at eastern South China Block (SCB) (Figure 1.0-1).
Test Data
Results
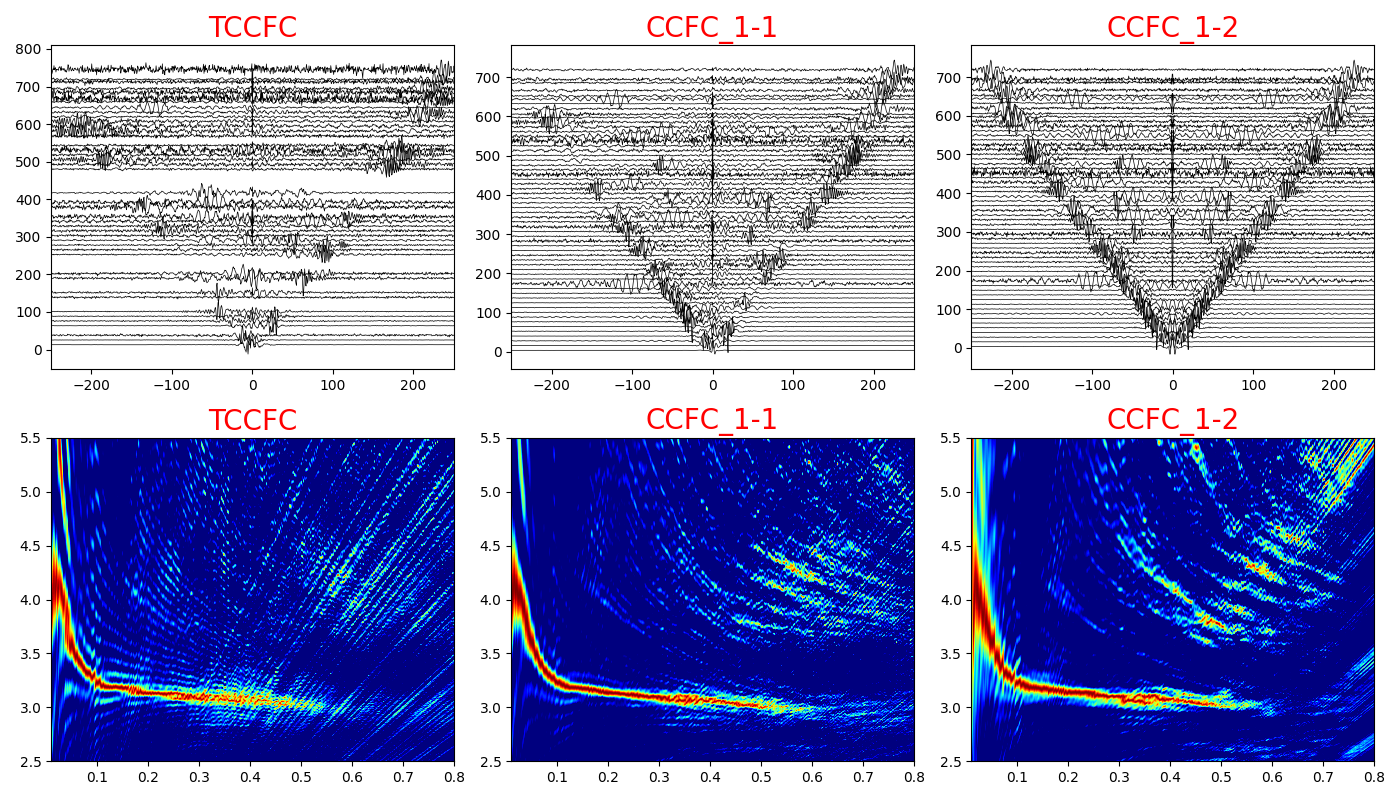
- We can see that the SNR of the fundamental mode is significantly improved, and several multimodal strips have clearly appeared in the time domain CCFs.
- In terms of the dispersion spectrogram, the overtones are much clearer after applying CCFC_1-1 and CCFC_1-2 compared to TCCFC.