Abstract
Recent satellite observations (2000–2020) have revealed interannual magnetic variations originating from Earth’s core. These variations have periods close to the Alfvén time scale (τₐ ≈ 2 years), much shorter than the core’s rotational period (τᵤ ≈ 150 years), suggesting they are not caused by core rotation. Instead, recent studies (Gillet et al., 2021) suggest that these variations are likely due to Magnetic-Archimedes-Coriolis (MAC) waves, a type of magneto-hydrodynamic wave propagating within the core. This study aims to study the propagation and dispersion of MAC waves to better understand planetary magnetic field variations. By matching numerical simulations with geomagnetic variation observations, we can also infer physical properties of the outer core.
MAC waves result from perturbations in the liquid outer core, driven by the interaction of Lorentz force, Coriolis force, and buoyancy due to temperature gradients. Given the complexity of the governing equations and the nonlinearity of the core’s properties, a full theoretical solution is difficult. Therefore, this study will build a MATLAB program to simulate MAC waves, based on Prof. Yufeng Lin’s previous work on MC waves. Using spherical harmonic analysis and a simplified core model, the simulation will help identify possible surface-recorded waveforms and uncover their underlying patterns.
Equations
Here, I only present the core equations. Detailed derivations and assumptions of these equations can be found in (Buffett et al., 2016).
\[\left\{ \begin{aligned} \frac{\partial \vec{u}}{\partial t} + 2(\vec{\Omega} \times \vec{u}) &= -\frac{1}{\rho} \nabla p + \frac{1}{\rho \mu_0} (\nabla \times \vec{b}_0) \times \vec{B}_0 + \nu \nabla^2 \vec{u} - \alpha g \Theta r \hat{r} \\ \frac{\partial \vec{b}}{\partial t} &= \nabla \times (\vec{u} \times \vec{B}_0) + \eta \nabla^2 \vec{b} \\ \frac{\partial \Theta}{\partial t} + \vec{u} \cdot \nabla T(r) &= \kappa \nabla^2 \Theta \\ \end{aligned} \right.\]This study utilizes harmonic analysis to numerically model the linearized physical equations. By solving the corresponding eigenfunctions, we can simulate the theoretical geomagnetic variation patterns of different eigenmodes to match with the observations. Details of the governing equations and parameter selection can be found in (Lin & Ogilvie, 2017).
Numerical Results Compared to Observations
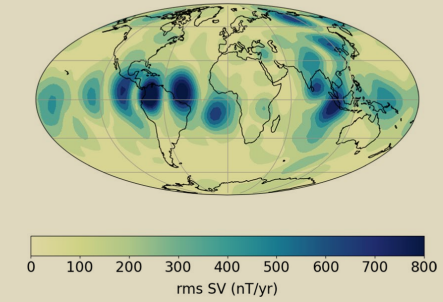
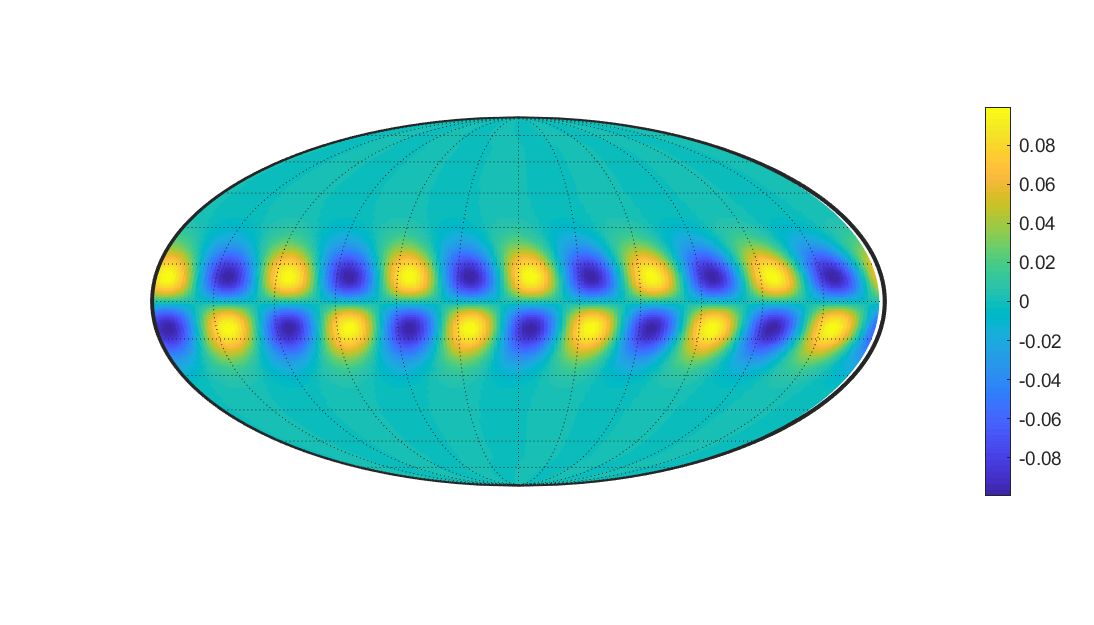
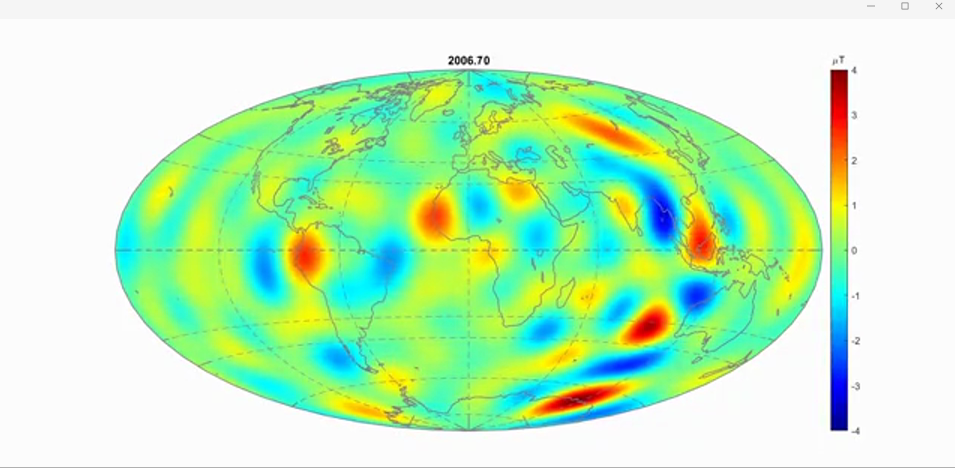
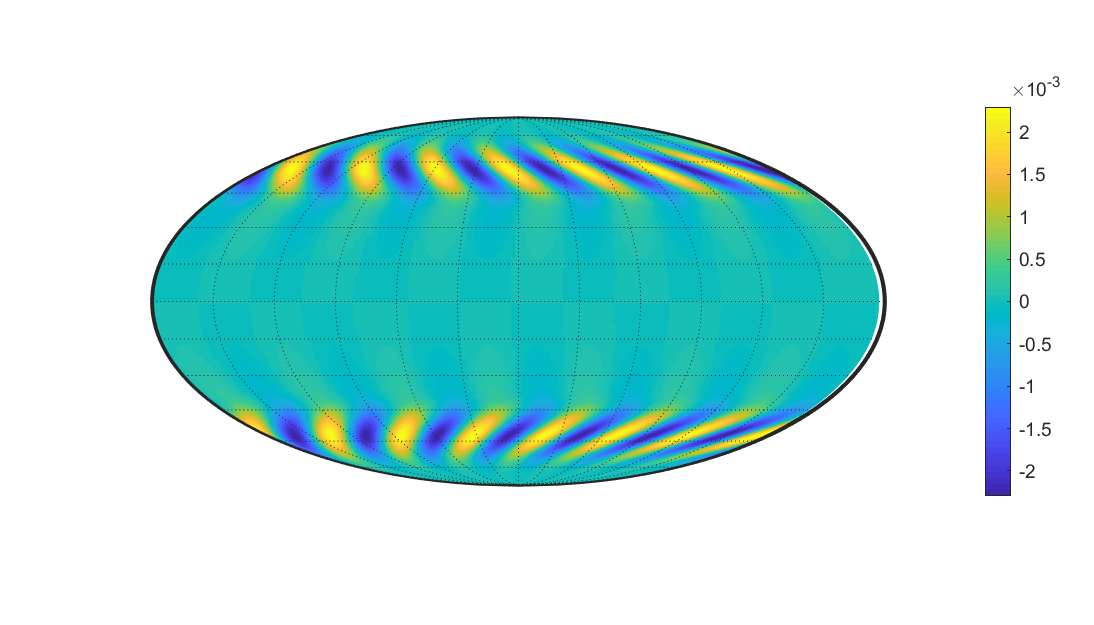
Breif Summary
-
From the numerical simulation results, it can be observed that the theoretically detectable waveforms, with small time decay around 𝑚=6 and 𝑚=7, show a certain degree of correlation with actual observations near the equator and in mid to high latitudes. This partly confirms that the propagation of MAC waves, induced by the adiabatic layer at the top of the outer core, is likely the main cause of the annual magnetic variations observed by satellites.
-
At higher frequencies (near 𝑤=0.6), the waveforms are primarily controlled by the Coriolis force, propagating along the axis of rotation and predominantly along mid to high latitudes. Numerical simulations have also corroborated this. Therefore, the annual magnetic variations observed in mid to high latitudes are likely due to the propagation of high-frequency MAC waves.
-
At lower frequencies (around 𝑤=0.001), the effects of buoyancy induced by temperature gradients and the influence of the magnetic field gradually strengthen, showing characteristics of propagation along lower latitudes. Numerical simulations confirm this. Thus, the annual magnetic variations observed in the equatorial and mid to low latitudes are likely due to the propagation of low-frequency MAC waves.